Helix World +

Theory of electric and magnetic field in electromagnetic waves

１　Electromagnetic waves have no electric field 　　　　　　　　　　 − 日本語 − 　　 ＜Reference 王様は裸＞

２　Unclear about radio waves 　　　　　　　　　　　　　　　　　　− 日本語 −

３ Form of current　　　　　　 　　　　　　　　　　　　　　　　　 　　 − 日本語 − ＜Reference Comment＞

４ Electrical and Magnetic forces　　　　　　　　　　　 　　 　− 日本語 −

５ Electromagnetic waves are traveling magnetic fields 　　　　　　　− 日本語 −

６ Generate electromagnetic waves 　　　　　　　　　　　− 日本語 −

７ Receive electromagnetic waves 　　　　　 　　　　　　− 日本語 −

８ Polarization 　　　　　　　　　 　　　　　 　　　　　　 − 日本語 −

９ Insertion device for synchrotron　　　　　　 　　　　　　　　　　 　　 　− 日本語 −

１０ Longitudinal and Transverse Waves 　　　　　　　　　　　 　　　　　− 日本語 −

１１　Vibration of string　　　　　　　　　　　　　　　　　　　 − 日本語 −

Apr./20/2025

＜ 1　Vibration of a pendulum ＞

　Figure 1 shows how a pendulum with a weight suspended by a wire or a spring vibrates.

The left end of Figure 1 shows a basic pendulum with a weight suspended by a wire, which swings the weight horizontally.

If the wire is made into a spring, it can also vibrate in the vertical direction. Furthermore, if the vibration period and phase of the spring and pendulum are synchronized, the orbit of the weight will be as shown in the figure. The linear and elliptical orbits shown in the figure are typical examples.

　

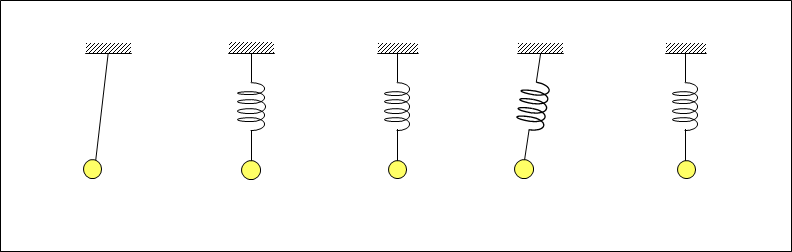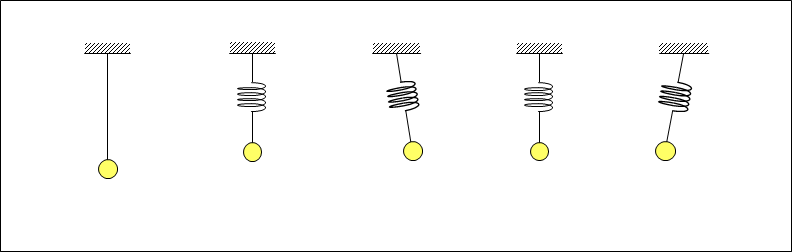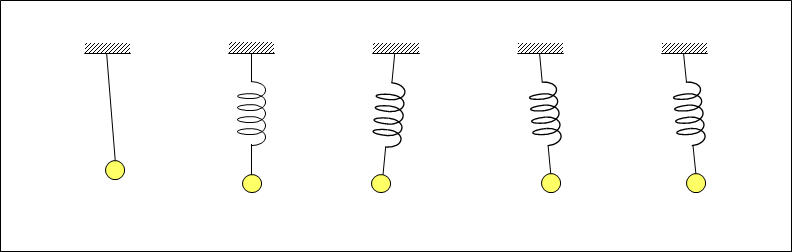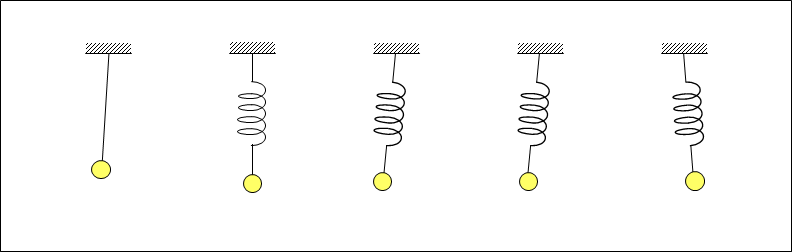
In the basic vibration of a pendulum, kinetic energy from the velocity and mass of the swinging weight in the horizontal direction and potential energy from the height and mass of the lifted weight are alternately converted. Then, the energy is conserved and the vibration is repeated as a pendulum. The phase of the change in velocity of the weight, which increases or decreases kinetic energy, and the phase of the vertical movement of the weight, which increases or decreases potential energy, are offset by 1/4 cycle of the pendulum's vibration period.

When the wire of the pendulum is made into a spring, the vibration of the vertical weight due to the extension and compression of the spring is added to the vibration of the vertical weight due to the pendulum, forming the vibration shown in Figure 1.In this case, kinetic energy from the velocity of the moving weight and its mass, potential energy from the height of the weight and its mass, and elastic energy from the extension and compression of the spring are alternately converted. Then, the vibration is repeated with the energy conserved. The phase of the change in velocity of the weight, which increases or decreases kinetic energy, and the phase of the extension or compression of the spring, which increases or decreases elastic energy, are offset by 1/4 cycle of the vibration period.

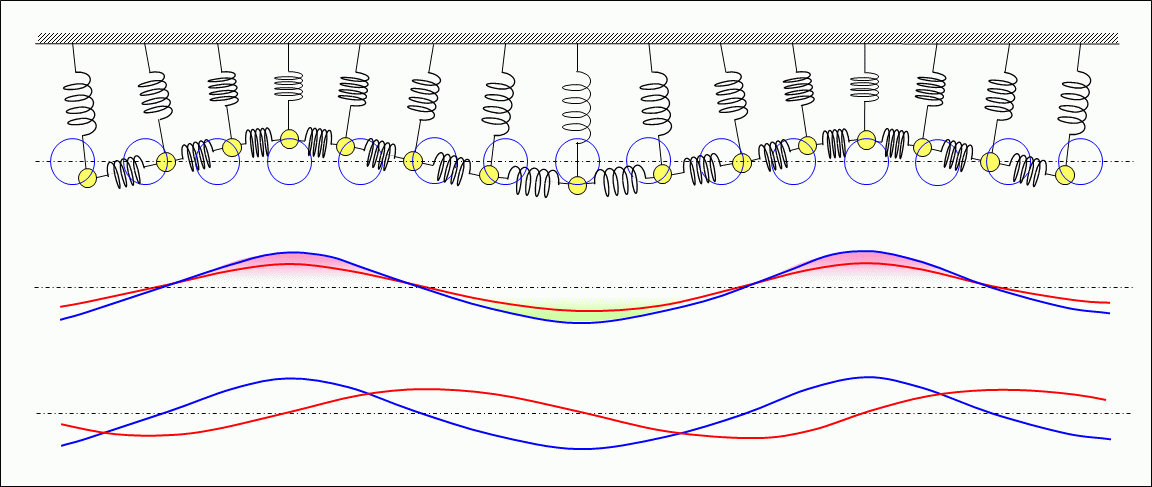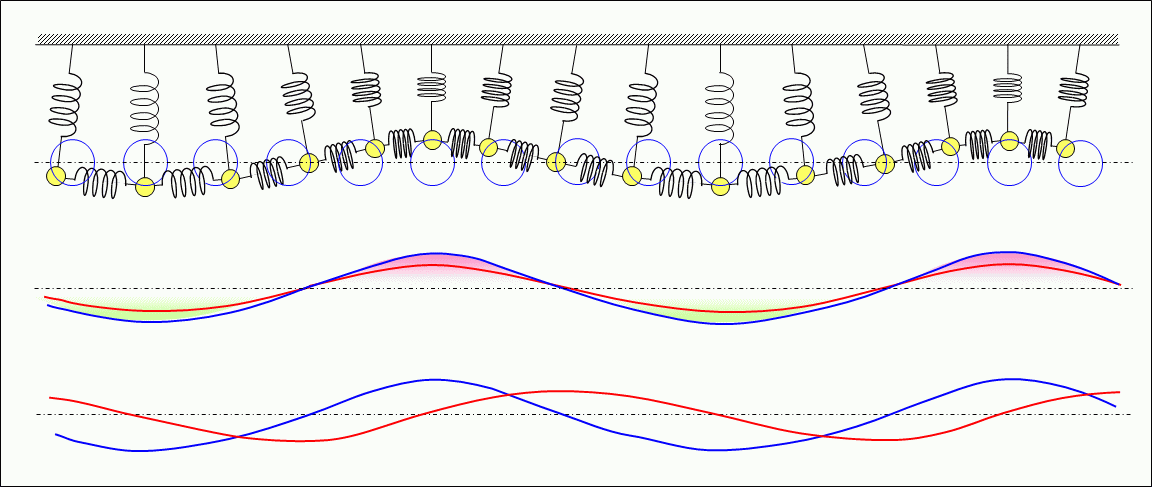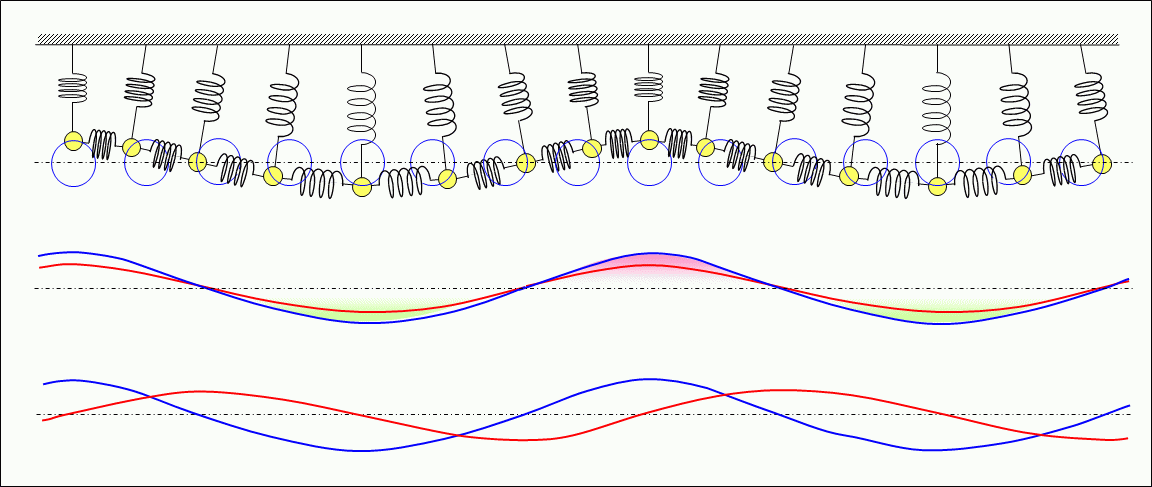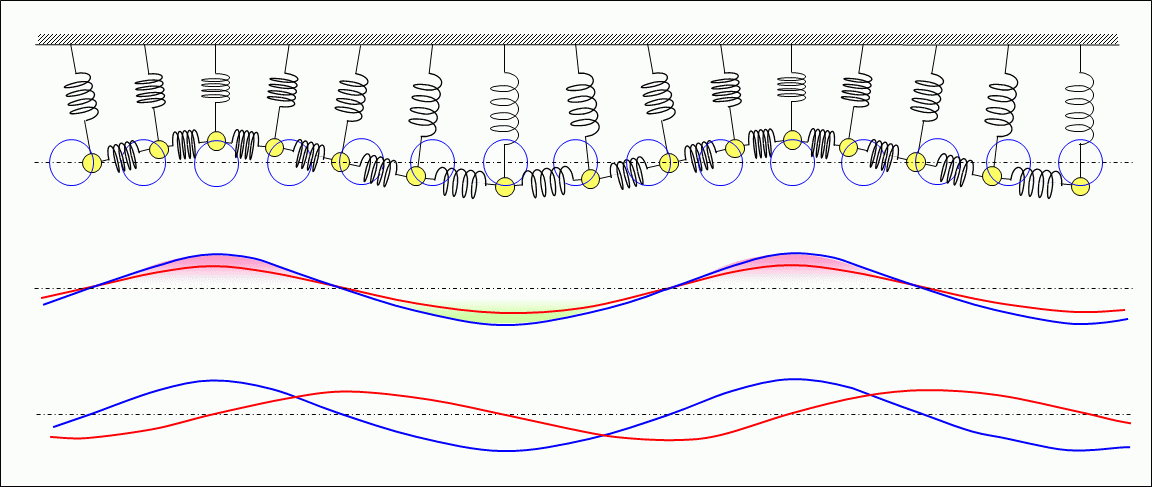
If several springs and weights shown in Figure 1 are lined up, each weight suspended by spring V and connected to the adjacent weights by spring H, vibration can be propagated as shown in Figures 2 and 3.

Figure 2 shows the traveling wave formed by the multiple springs and weights.

　

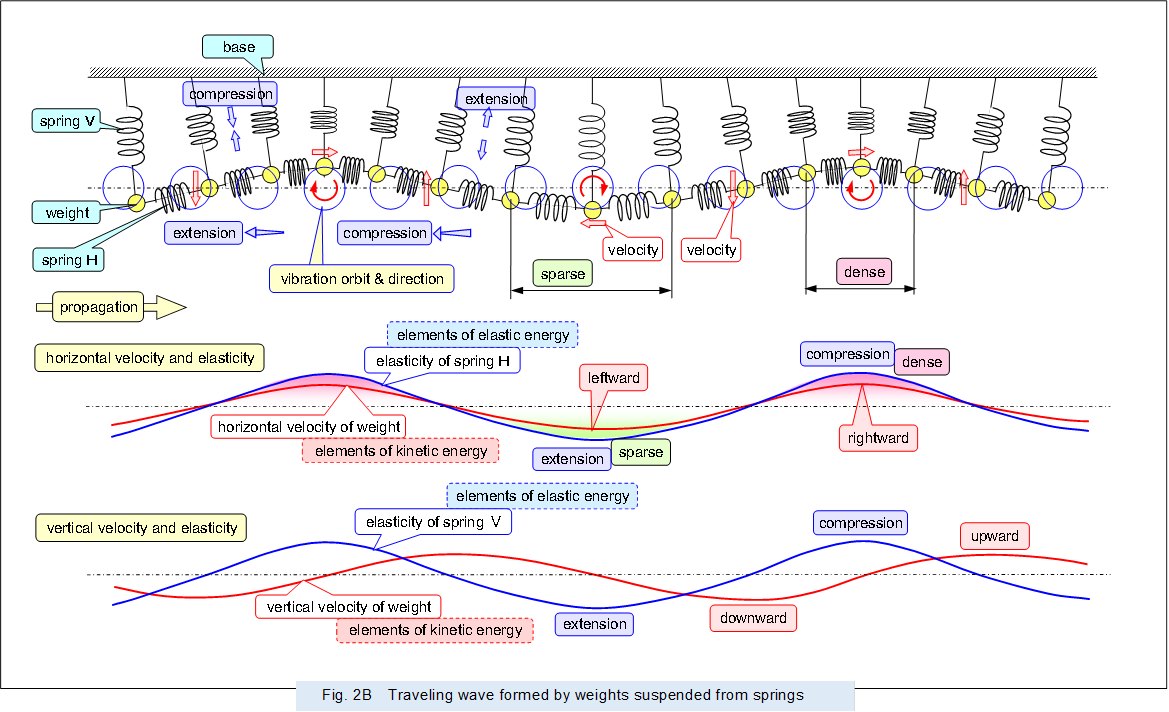As described above, the wave is a transverse wave with orthogonal vibration to the direction of propagation (horizontal direction). However, as the middle section, “horizontal velocity and elasticity” indicates, the phase in which the velocity of the weight moving in the horizontal direction changes and the phase in which the spring extends and compresses are in phase, forming a longitudinal traveling waves. The energy is propagated in the direction of propagation by both the kinetic energy from the velocity and mass of the moving weight and the elastic energy preserved by the spring. As shown in “vertical velocity and elasticity” in the lower section, the phase of the change in the velocity of the vertically moving weight and the phase of the extension and compression of the spring are offset by 1/4 cycle of the vibration period, forming a standing wave.

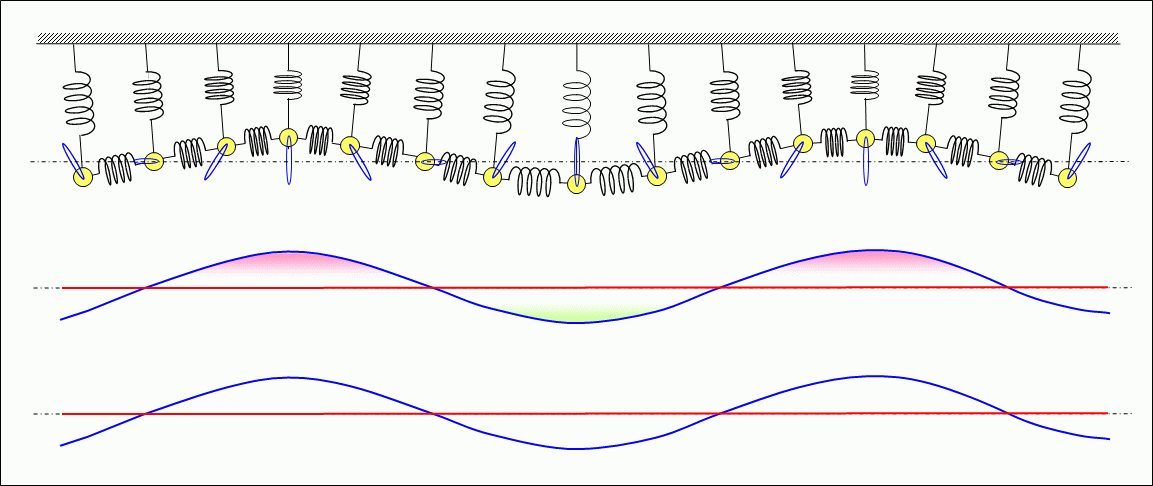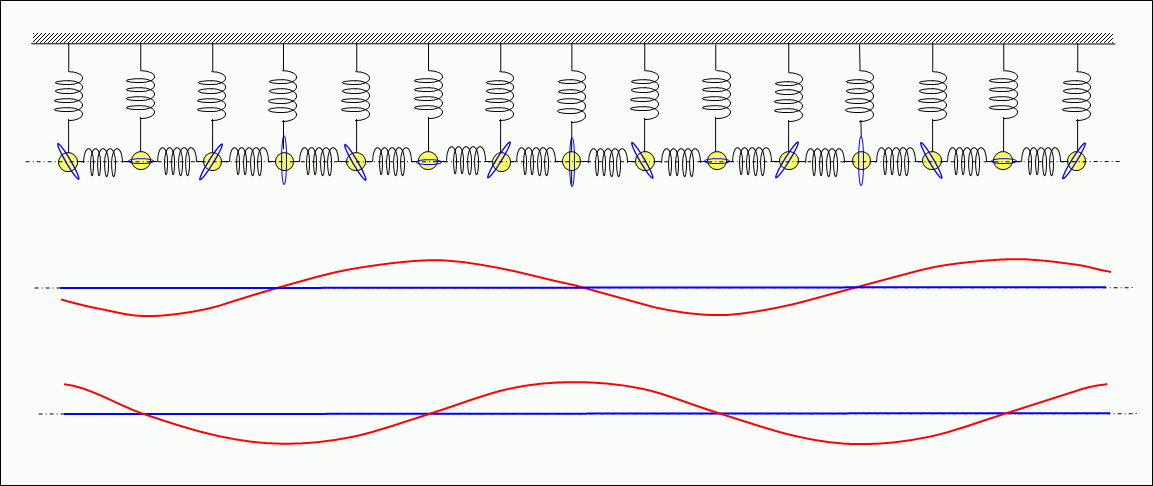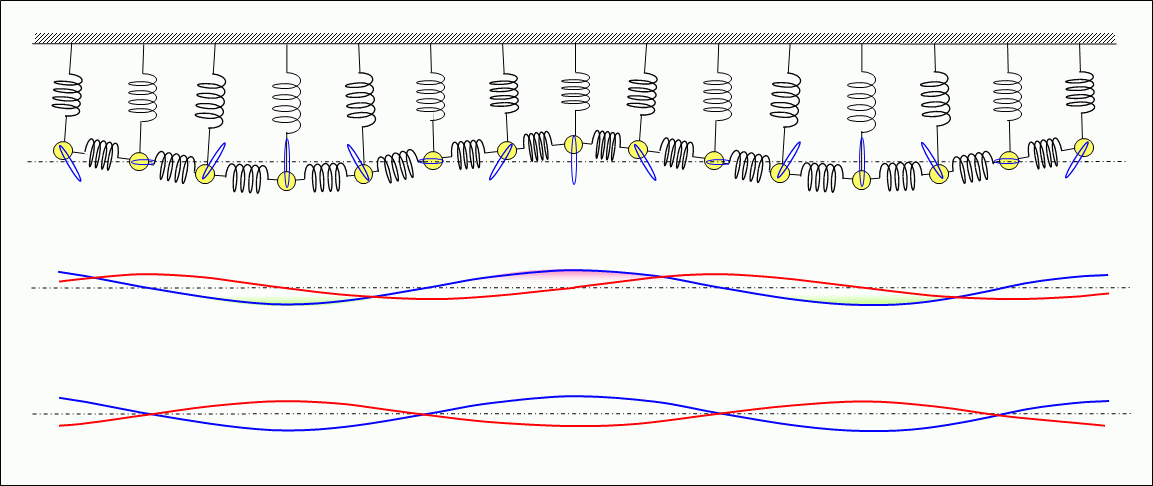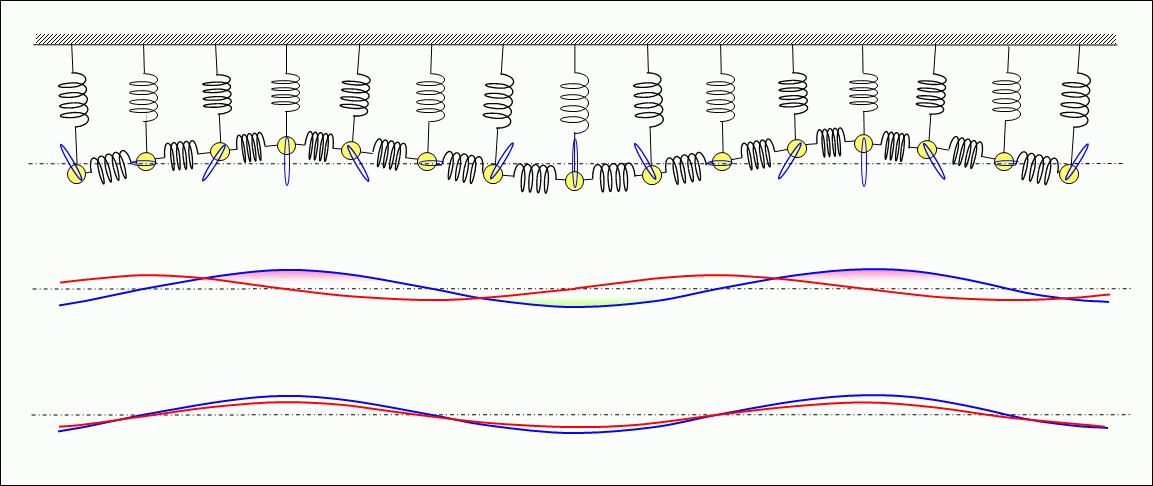
Figure 3 shows the standing waves formed by multiple springs and weights.

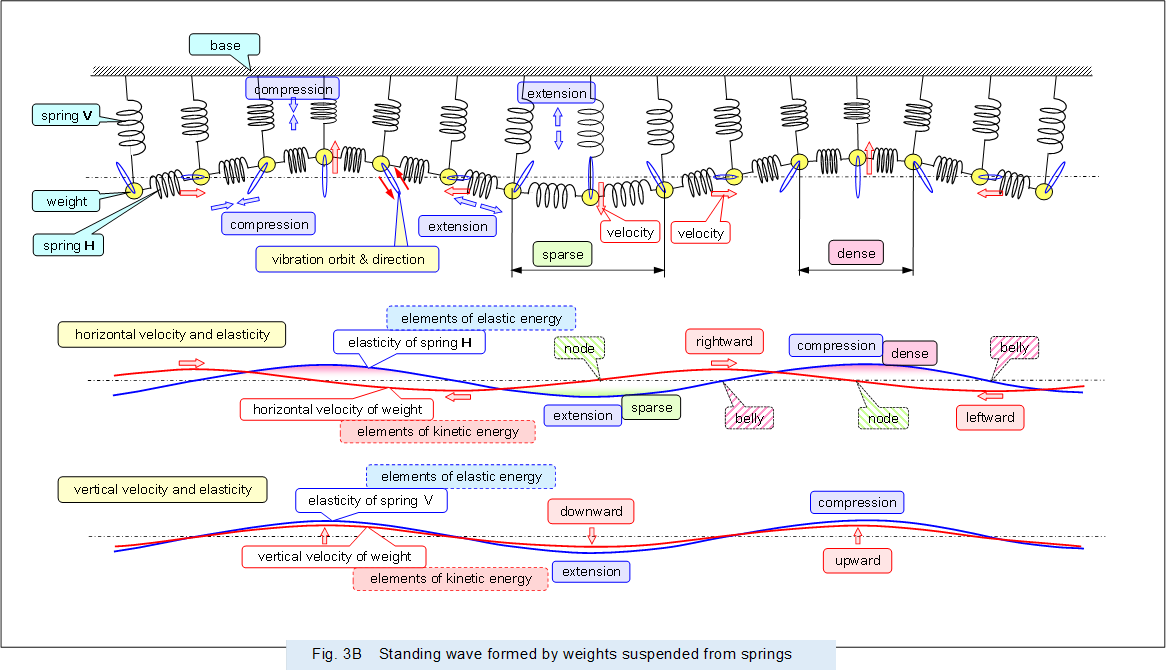As described above, this wave is a transverse wave with vibration orthogonal (vertical) to the direction of propagation (horizontal direction). The phases of the change in the velocity of the weight in the horizontal direction and the phase of the extension and compression of the spring (shown in “horizontal velocity and elasticity” in the middle) and the phase of the change in the velocity of the weight in the vertical direction and the phase of the extension and compression of the spring (shown in “vertical velocity and elasticity” in the lower) are both offset by 1/4 cycle of the vibration period,, forming a standing wave. Then, in both the vertical and horizontal directions, energy is alternately converted from the kinetic energy of the weight to the elastic energy of the spring or from the elastic energy to the kinetic energy, in other words, one energy is alternately converted to another energy, and by repeating this process, the energy is preserved in that place. In the horizontal direction, longitudinal waves are formed.

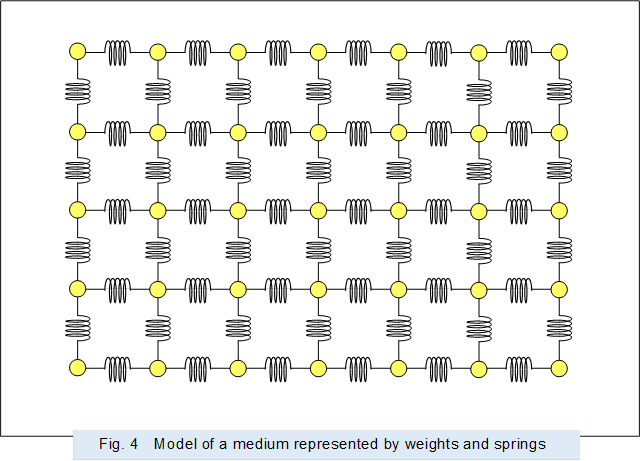
Figure 4 shows a model of a medium simulated by multiple weights and springs connecting the weights. In this model, the mass of the weights corresponds to the mass of the medium and the elasticity of the spring corresponds to the elasticity of the medium, and gas, liquid, and solid can be modeled by appropriately selecting the mass of the weights and the elasticity of the spring. Then, it is possible to simulate the vibration or wave propagating in the medium.

The orbits of the vibrating weights, shown above as straight lines or ellipses including circles as examples, will be appropriate to the physical characteristics of the medium, such as gas, liquid, or solid, and to the magnitude of the vibrations.

For reference, if the weights and springs in the above model correspond to the Proximity effects between free electrons in a conductor, they can be applied to describe the current formed by the longitudinal waves of electrons described in the “Form of current” section above.

The wave is formed by the kinetic energy due to the moving velocity of the weight and its mass, the elastic energy, the potential energy, and the density energy, etc., as described above, and energy is propagated by both the kinetic energy and the other energy. Alternatively, it preserves energy in that place by alternately converting the kinetic energy and the other energy, and is not formed by either energy alone.

＜ 2　Vibration of a stringed instrument ＞

　Figure 5 shows an outline of a string and other key parts of an acoustic stringed instrument.

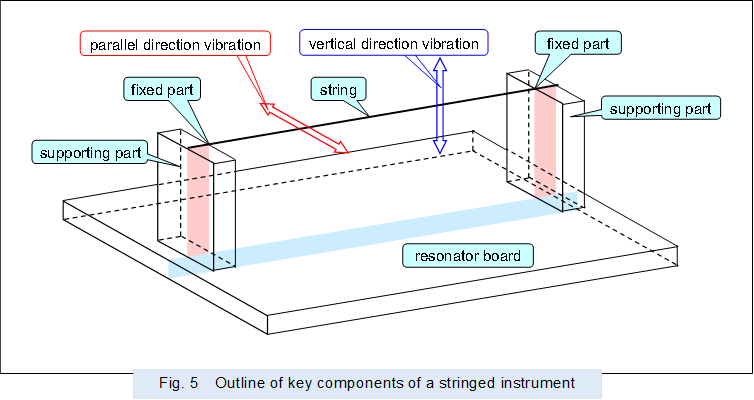Figure 6 shows a cross-section of a string and key parts of Figure 5.

　 Figure 7 shows the string in Figure 6 by weight and springs as above.

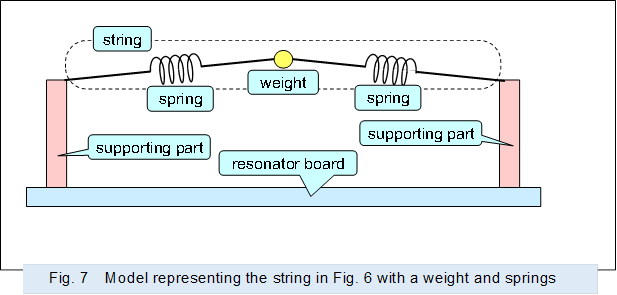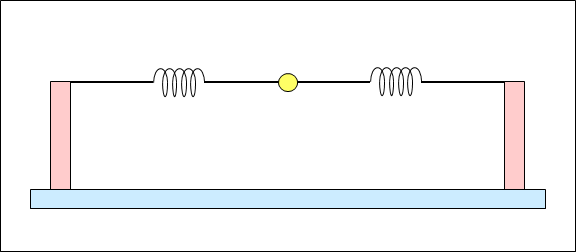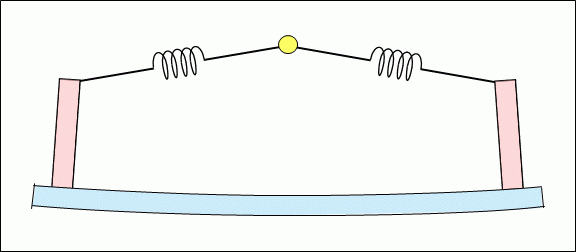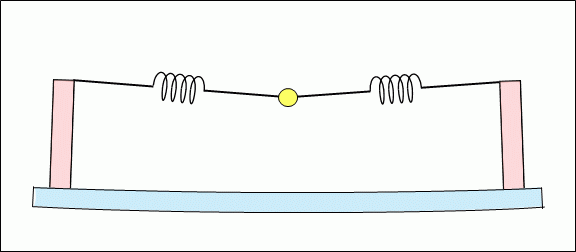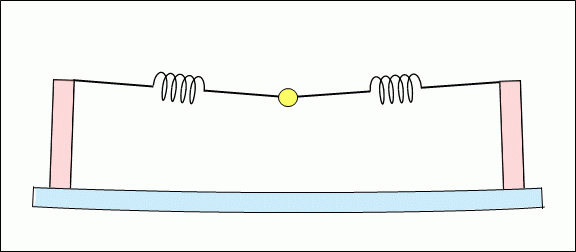
Figure 8 shows each part of the model in Figure 7 vibrating.

　

As described above, the resonator board of an acoustic stringed instrument contains vibrations (harmonics) with a double frequency to the vibration (reciprocating motion) of a string. Then, they are synthesized with the basic wave of the strings to produce the unique tone of each stringed instrument.

In addition, an electric guitar that is power-assisted does not have a resonator board that an acoustic instrument has, as shown in Figure 9, which shows a string, a pickup sensor, and key parts. However, an electric guitar also produces the same doubled harmonics as an acoustic stringed instrument and produces the same scaled tones, and the reason why the doubled harmonics are produced is considered.

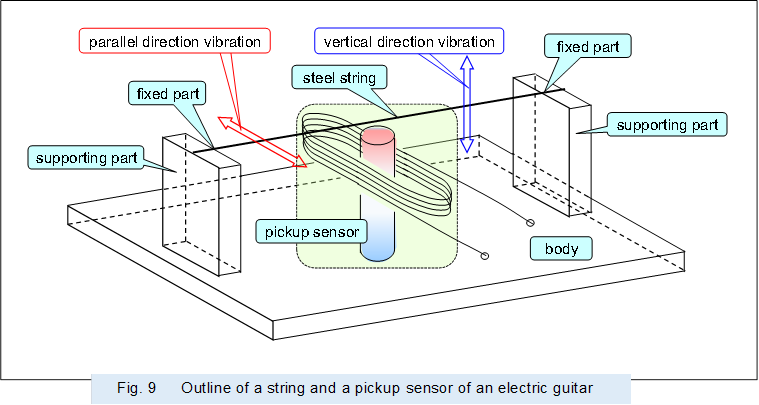Figure 10 shows the magnetic field formed by a string vibrating vertically to the body (resonator board) (axially approaching/leaving the magnets in the pickup sensor) and a pickup sensor.

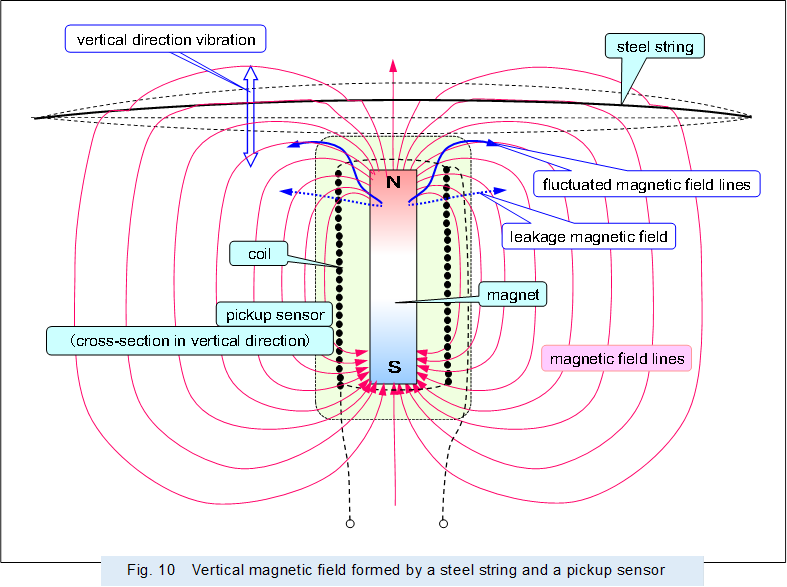As described above, there are magnetic field lines leaking from the sides of the coil in the pickup sensor of an electric guitar. When the iron string vibrates vertically to the body (resonator board), if the string approaches the magnet, the magnetic field lines are concentrated due to the decrease in magnetic resistance at the coil aperture, and the magnetic field lines that were leaking from the sides described above are directed toward the coil aperture and pass through the coil aperture. On the other hand, if the string leaves the magnet, the magnetic resistance of the coil aperture increases and the magnetic field lines return to their original path, increasing the magnetic field lines leaking from the sides of the coil.

In other words, when the string approaches, the magnetic field lines chaining the coil increase and the output current of the coil increases, and when the string leaves, the magnetic field lines chaining the coil decrease and the output current of the coil decreases. Therefore, the output current of the pickup sensor increases or decreases once for each reciprocation of the string, so the current corresponding to the basic wave of the string is output.

Figure 11 shows the magnetic field formed by a string vibrating parallel to the body (resonance board) (approaching/leaving the axis of the magnets in the pickup sensor from the transverse direction) and a pickup sensor.

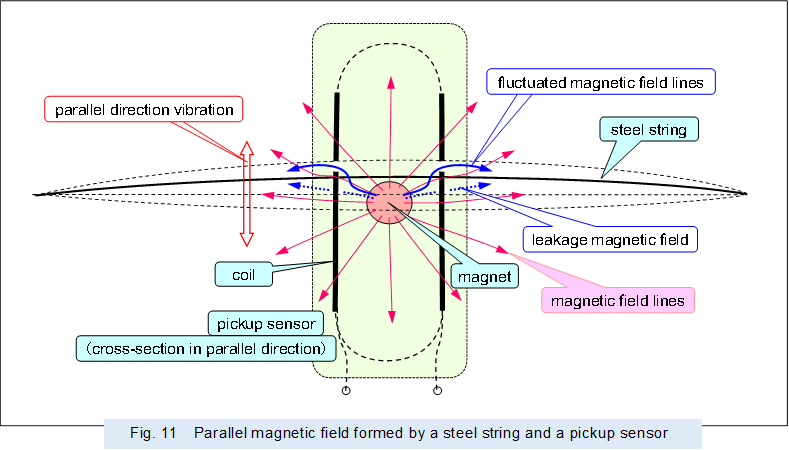As described above, in the pickup sensor of an electric guitar, when the iron string vibrates in a parallel direction to the body (resonator board), if the string approaches the axis of the magnet, the magnetic resistance of the aperture of the coil decreases and the magnetic field lines concentrate, and the magnetic field lines that were leaking from the sides described above are directed toward the aperture of the coil, and pass through the coil apertures. On the other hand, if the string leaves the axis of the magnet, the magnetic resistance of the coil aperture increases, the magnetic field lines return to their original path, and the magnetic field lines leaking from the sides of the coil increase.

In other words, when the string approaches the axis of the magnet, the magnetic field lines chaining the coil increase and the output current of the coil increases, and when the string leaves, the magnetic field lines chaining the coil decrease and the output current of the coil decreases.

However, the coil outputs same volume and same polarity of current whether the string approaches from above or below the axis of the magnet as shown in the figure.

Therefore, the output current of the pickup sensor increases or decreases twice for each reciprocation of the string, so the current corresponding to double the harmonics of the string's basic wave is output.

The electric guitars' pickup sensors, which are power-assisted as described above, do not faithfully convert string vibrations to electric current like Ribbon-type microphones, but have unique characteristics that produce tones on the same scale of an acoustic stringed instrument. In addition, depending on the technique of playing and the characteristics of the pickup sensor, output the electric guitar's unique tones.

＜ 「Longitudinal and Transverse Waves」・